LadderLeak, comment retrouver une clef privée ECC sur analyse de consommation électrique

Le LadderLeak est une attaque par canaux auxiliaires permettant de retrouver une clef privée lors d’opérations de chiffrement sur courbes elliptiques. Cet article a pour but d’expliquer en détails cette attaque, ses limites pratiques et les solutions qui existent pour s’en protéger.

ECC ou Ellipitic Curves Cryptography

La cryptographie sur courbes elliptiques (ECC) est un protocole de chiffrement asymétrique comme RSA ou Diffie-Hellman, qui se base sur les propriétés mathématiques des courbes elliptiques. Ces courbes sont définies par une équation qui peut prendre plusieurs formes, comme les équations de Weierstrass: $Y^2 = X^3 + aX + b$

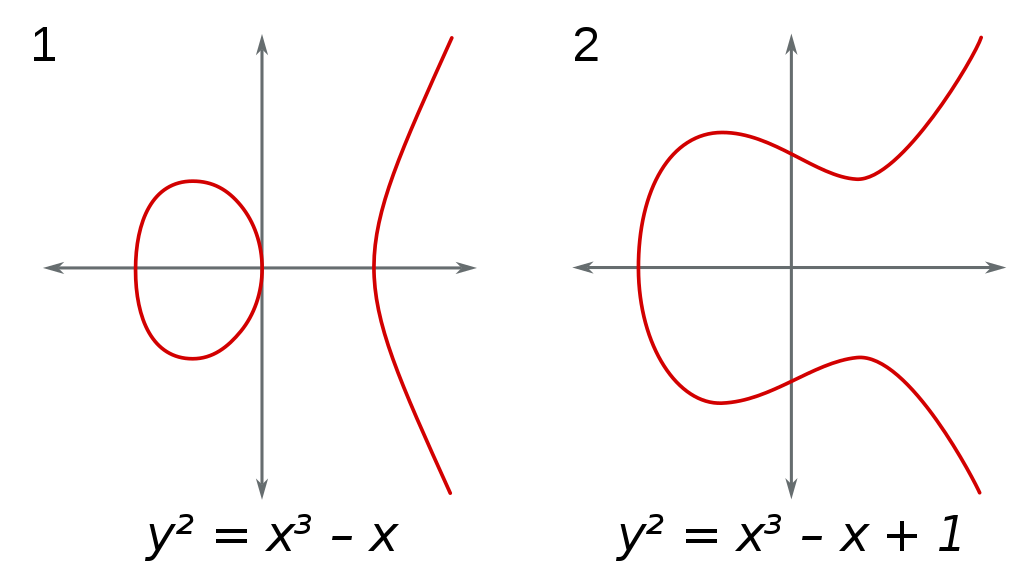
Sur cet exemple la courbe 1 a pour coefficients a = -1 et b = 0, et la courbe 2, a = -1 et b = 1. L’ensemble des solutions d’une équation définissent les points de la courbe sur lesquels travailler. Sur chacun de ces points, il est possible de définir des opérations d’addition et de multiplication.

Ladder: la multiplication scalaire de points

Pour deux points sur la courbe, prendre leur somme donne un troisième point, lui aussi sur la courbe. Répéter l’addition d’un même point avec lui-même revient à faire une multiplication dite scalaire. Cette multiplication est une opération mathématique à sens unique, pour deux points R et P connus, on ne peut pas retrouver la clef privée (un entier) n tel que R = nP. C’est ce qu’on appelle une trapdoor function, un principe mathématique facile à calculer dans un sens, mais très dur voire impossible à faire dans l’autre sens. Ce principe de one-way fournit la sécurité sur laquelle se base la cryptographie sur courbes elliptiques.

Note: Pour avoir un bon aperçu visuel des opérations menées sur les courbes elliptiques, je conseille ce site https://curves.xargs.org/

L’algorithme de multiplication scalaire se définit comme ceci pour un point P et un scalaire n (qui est la clef privée du cryptosystème) tels que R = nP:

Q := P and R := O.
for each bit in n; do.
    if bit = 1; then
        set R = R + Q
  
    set Q = 2Q.
done
return the point R

Temps constant ou pas, quelle différence ?

Comme on peut le voir ci-dessus, l’algorithme de multiplication scalaire ne se fait pas en temps constant pour deux n différents puisque cette méthode fait un calcul supplémentaire lorsque le bit en $i_{ème}$ position est à 1.

Ça n’a pas l’air alarmant comme cela, mais un algorithme qui n’est pas en temps constant peut faire fuiter de l’information. Par exemple calculer pour n = 0b11111111 prendra 7 opérations de plus que pour n = 0b10000000. Généralisé sur des nombres de plusieurs centaines de bits, de telles différences peuvent se voir au temps d’exécution auquel cas il deviendrait possible de faire des hypothèses sur le nombre de bits set dans le scalaire.

Le principe de l’attaque

Comme cet algorithme n’effectue pas le même nombre d’opérations en fonction du bit, ce comportement se répercute non-seulement au niveau temporel mais surtout au niveau de consommation électrique. Moins de calculs entraîne moins de puissance CPU donc moins d’énergie consommée. Le LadderLeak, c’est ça: étudier la consommation CPU d’un ordinateur qui calcule une multiplication scalaire lors d’un chiffrement sur courbes elliptiques pour en déduire la clef privée utilisée.

Exemple

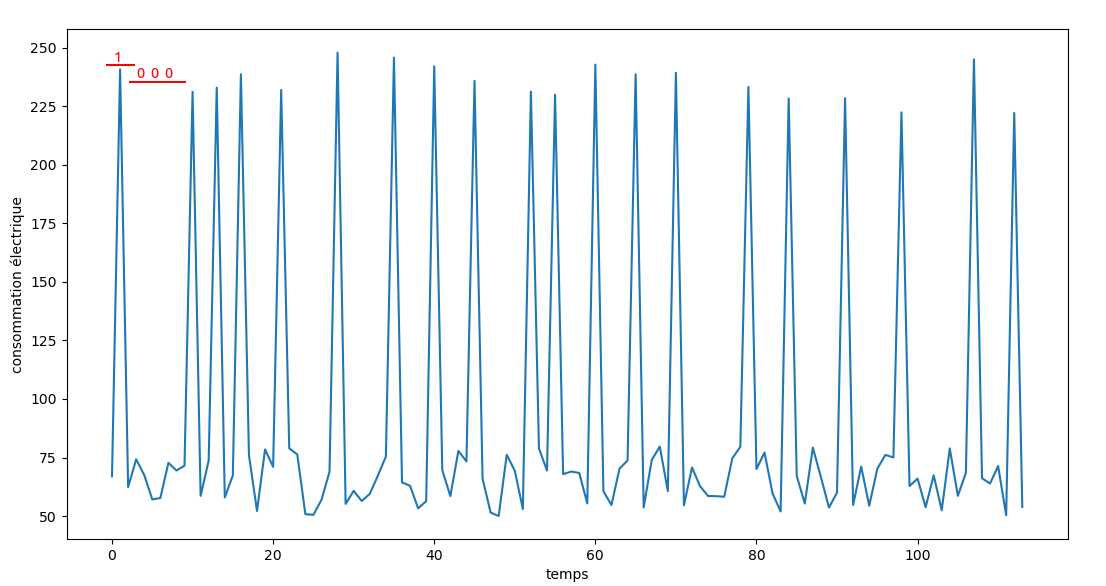
En utilisant la clef privée GISTRE convertie en entier pour chiffrer des messages sur la secp256k1, on obtient le graphe de consommation électrique suivant sur lequel on peut voir très clairement les pics d’énergie sur lesquels une opération supplémentaire a été réalisée.

#

On peut donc facilement deviner que le début de la représentation binaire de la clef privée est 01000111 soit G en binaire.

Comment se protéger de cette attaque ?

Seules les courbes définies par une équation de Weierstrass et leur implémentation de multiplication scalaire en temps inconstant sont vulnérables. Cependant, certaines courbes admettent des propriétés très intéressantes permettant de mapper les points sur une courbe différente mais qui possède un algorithme de multiplication en temps constant. Ces courbes peuvent prendre des formes différentes comme les courbes de Montgomerry définies par l’équation $BY^2 = X^3 + aX^2 + X$. On dit de ces courbes qu’elles admettent des équivalences birationnelles à leurs jumelles car il existe des formules pour passer de l’une à l’autre.

Seulement, ces formules n’existent pas toujours. En effet, certaines courbes comme la secp256k1 ne possèdent pas de telles propriétés car elles sont d’ordre premier, ce qui fait qu’il est impossible de mapper ces courbes sur leur forme de Montgomerry puisque celles-ci doivent avoir un ordre divisible par 4 ce qui est impossible pour un nombre premier CQFD!

Quel est la portée de cette attaque ?

Il est intéressant de noter que le Bitcoin utilise la courbe secp256k1, qui est vulnérable à cet exploit et pourtant, personne n’a réussi à utiliser cette technique pour détourner de l’argent. C’est là qu’on voit les limites pratiques de l’attaque, pour mettre cela en pratique il est nécessaire d’avoir un accès physique aux machines concernées pour pouvoir analyser les consommations électriques. Comme le Bitcoin est décentralisé, il est extrèmement difficile de prévoir sur quelle machine les calculs se feront et sûrement encore plus d’y acccéder.

De votre côté, il n’y a rien à faire mis à part se renseigner sur les libcrypto que vous utilisez. Celles-ci se chargent dans votre dos d’effectuer ces calculs en temps constant pour éviter ce genre de fuite d’information quand cela est possible. Cependant, il en existe certaines qui admettent que leurs implémentations sont imparfaites à ce niveau-là comme la crate `rsa vulnérable à la Marvin Attack. C’est donc important de toujours rester vigilant quant aux outils que vous utilisez, surtout si la sécurité de vos données est en jeu!

Sources